Teorema de Pitágoras: Demostración y Aplicaciones

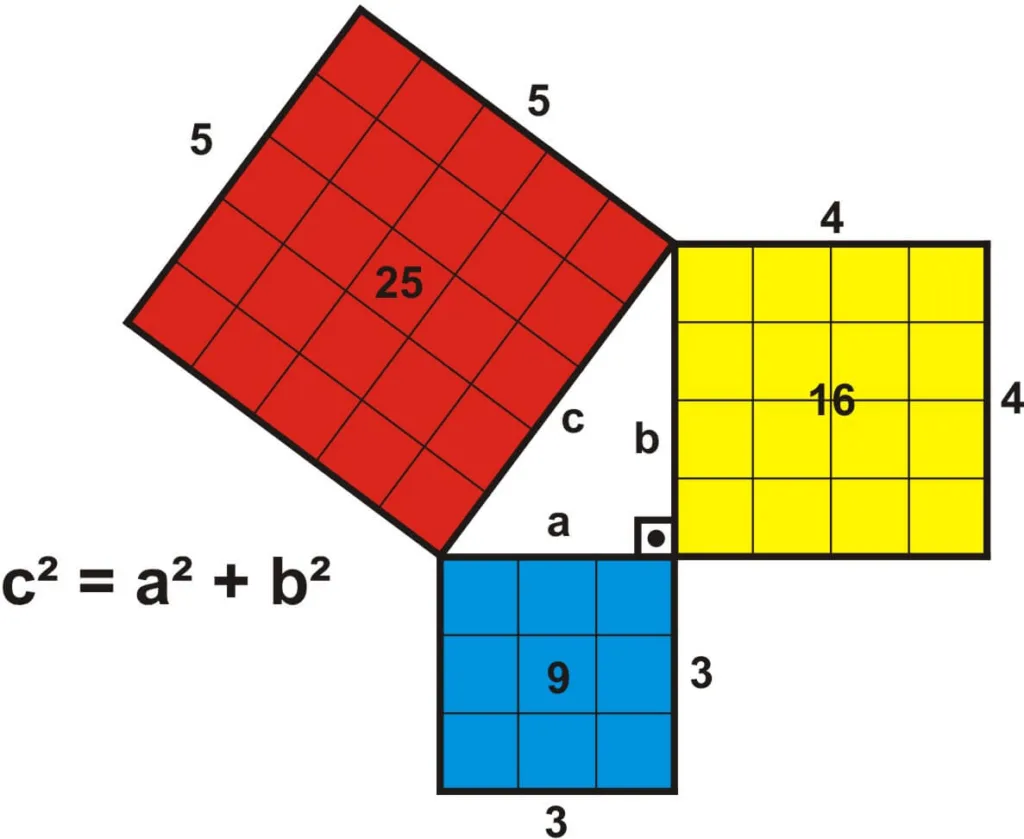
El teorema de Pitágoras es una proposición matemática fundamental que ha sido objeto de estudio y aplicación desde la antigüedad. Este teorema, nombrado en honor al filósofo griego Pitágoras, se refiere a las relaciones entre los lados de un triángulo rectángulo. En términos más simples, el teorema establece que la suma de las áreas de los cuadrados construidos sobre los catetos (los dos lados menores) es igual al área del cuadrado construido sobre la hipotenusa (el lado mayor). Este concepto no solo tiene relevancia en el ámbito académico, sino que también se aplica en diversas situaciones prácticas de la vida cotidiana.

El contenido de este artículo abordará la historia del teorema de Pitágoras, su demostración lógica y rigurosa, las aplicaciones prácticas, los métodos de demostración, los términos matemáticos asociados y un ejemplo práctico para ilustrar su uso.

Historia del Teorema de Pitágoras

El teorema de Pitágoras tiene sus raíces en la antigua Grecia, específicamente en la escuela pitagórica, una corriente filosófica y matemática que permitía el estudio de las matemáticas tanto a hombres como a mujeres. Pitágoras, el filósofo griego del siglo VI a.C., es conocido por su contribución a la geometría y la aritmética. Aunque no se tiene un registro exacto de cuándo se descubrió el teorema, se cree que fue durante los primeros años de la escuela pitagórica.

El teorema de Pitágoras ha sido demostrado y aplicado en diversas culturas a lo largo de la historia. Por ejemplo, en Egipto, el papiro de Ahmes (c. 1650 a.C.) contiene un problema que implica el uso del teorema de Pitágoras. En la India, los textos de Baudhayana (c. 800 a.C.) y los Sulbasutras también mencionan el teorema. Esto demuestra que el conocimiento de las relaciones entre los lados de un triángulo rectángulo ha sido compartido y utilizado en diferentes partes del mundo.

Escuela Pitagórica

La escuela pitagórica fue una corriente filosófica y matemática que permitía el estudio de las matemáticas tanto a hombres como a mujeres. Esta escuela se caracterizaba por su enfoque místico y espiritual hacia las matemáticas, viendo en ellas una forma de entender el universo. La escuela pitagórica también fue pionera en la idea de que los números son la base de todas las cosas, lo cual es una visión que ha influido en el desarrollo de la matemática moderna.

Demostración Lógica y Rigurosa

El teorema de Pitágoras puede ser demostrado de manera lógica y rigurosa utilizando reglas y principios matemáticos. Una de las formas más comunes de hacerlo es mediante el uso del álgebra. Supongamos que tenemos un triángulo rectángulo con catetos de longitudes ( a ) y ( b ), y una hipotenusa de longitud ( c ). De acuerdo con el teorema de Pitágoras, se tiene que:

[ a^2 + b^2 = c^2 ]

Esta ecuación puede ser demostrada mediante el despliegue del triángulo en un cuadrado. Al hacer esto, se crean cuatro triángulos rectángulos adicionales, cada uno con lados de longitud ( a ) y ( b ). La suma de las áreas de estos cuadrados es igual al área del cuadrado construido sobre la hipotenusa.

Regletas de Montessori

Otra forma de demostrar el teorema de Pitágoras es utilizando regletas de Montessori. Estas regletas son piezas rectangulares que se pueden combinar para formar diferentes figuras geométricas. Al colocar las regletas en un patrón específico, se puede ver cómo la suma de las áreas de los cuadrados construidos sobre los catetos es igual al área del cuadrado construido sobre la hipotenusa.

Aplicaciones Prácticas

El teorema de Pitágoras tiene numerosas aplicaciones prácticas en la vida cotidiana y en diversas disciplinas. Una de las aplicaciones más comunes es en la construcción, donde se utiliza para calcular distancias y áreas. También es útil en la navegación, ya que permite determinar la posición de un barco o avión en relación con su punto de partida.

Medición de Distancias

En la medición de distancias, el teorema de Pitágoras se utiliza para calcular la longitud de una línea cuando se conocen las longitudes de los lados adyacentes. Esto es útil en la construcción de edificios y en la ingeniería civil. Por ejemplo, si se sabe que un triángulo tiene lados de 3 metros y 4 metros, y se quiere encontrar la longitud de la hipotenusa, se puede usar el teorema de Pitágoras para calcularlo.

Métodos de Demostración

Existen varios métodos para demostrar el teorema de Pitágoras. Algunos de los más comunes incluyen:

Álgebra

Como se mencionó anteriormente, una forma común de demostrar el teorema de Pitágoras es mediante el uso del álgebra. Esto implica la creación de un cuadrado con lados de longitud ( a ) y ( b ), y luego desplegarlo para formar un rectángulo con base ( c ).

Geometría

Otro método es mediante el uso de la geometría. Esto implica el dibujo de un triángulo rectángulo y luego la creación de un cuadrado con lados de longitud ( a ) y ( b ). Luego, se puede desplegar este cuadrado para formar un rectángulo con base ( c ).

Trigonometría

El teorema de Pitágoras también puede ser demostrado utilizando la trigonometría. Esto implica el uso de las relaciones entre los lados y los ángulos de un triángulo rectángulo para demostrar que la suma de las longitudes al cuadrado de los catetos es igual a la longitud al cuadrado de la hipotenusa.

Términos Matemáticos Asociados

El teorema de Pitágoras está asociado con varios términos matemáticos, incluyendo:

Catetos

Los catetos son los lados más cortos de un triángulo rectángulo. En el contexto del teorema de Pitágoras, se denotan comúnmente como ( a ) y ( b ).

Hipotenusa

La hipotenusa es el lado más largo de un triángulo rectángulo. En el contexto del teorema de Pitágoras, se denota comúnmente como ( c ).

Área

El área de un triángulo rectángulo puede ser calculada utilizando el teorema de Pitágoras. La fórmula para el área es:

[ text{Área} = frac{1}{2}ab ]

Donde ( a ) y ( b ) son las longitudes de los catetos.

Ejemplo Práctico

Para ilustrar el uso del teorema de Pitágoras, consideremos un triángulo rectángulo con catetos de 3 metros y 4 metros. Para encontrar la longitud de la hipotenusa, se puede usar la fórmula:

[ c = sqrt{a^2 + b^2} ]

Sustituyendo los valores de ( a ) y ( b ):

[ c = sqrt{3^2 + 4^2} ]
[ c = sqrt{9 + 16} ]
[ c = sqrt{25} ]
[ c = 5 text{ metros} ]

Por lo tanto, la longitud de la hipotenusa es 5 metros.

Conclusión

El teorema de Pitágoras es una herramienta matemática fundamental que tiene aplicaciones en diversas disciplinas y en la vida cotidiana. Su demostración puede ser realizada mediante varios métodos, incluyendo el álgebra, la geometría y la trigonometría. Los términos asociados con el teorema de Pitágoras incluyen los catetos, la hipotenusa y el área del triángulo rectángulo. Con un ejemplo práctico, se puede ver cómo el teorema de Pitágoras puede ser utilizado para resolver problemas matemáticos.