Métodos para dividir fracciones: Multiplicar en cruz vs Invertir y multiplicar

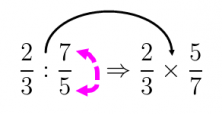
La división de fracciones es una operación matemática que puede resultar complicada para muchas personas. Sin embargo, existen varios métodos que pueden simplificar este proceso. En este artículo, exploraremos dos métodos comunes para dividir fracciones: el método de "multiplicar en cruz" y el método de "invertir y multiplicar". Ambos métodos son útiles y proporcionan resultados idénticos, permitiendo al usuario elegir el que prefiera.

El objetivo de este artículo es proporcionar una comprensión detallada de cada método, así como sus ventajas y desventajas. Además, se incluyen ejemplos prácticos para ilustrar cómo aplicar cada método en la vida cotidiana.

Método 1: Multiplicar en cruz

El primer método para dividir fracciones es conocido como "multiplicar en cruz". Este método implica multiplicar el numerador de la primera fracción por el denominador de la segunda y colocar el resultado en el numerador final. Por otro lado, se multiplica el denominador de la primera fracción por el numerador de la segunda y se escribe el resultado en el denominador final. Este método es intuitivo y fácil de recordar una vez que se comprende.

Para ilustrar este método, consideremos dos fracciones: (frac{a}{b}) y (frac{c}{d}). Para dividir estas fracciones, multiplicamos el numerador de la primera fracción ((a)) por el denominador de la segunda fracción ((d)), obteniendo (ad). Luego, multiplicamos el denominador de la primera fracción ((b)) por el numerador de la segunda fracción ((c)), obteniendo (bc). El resultado final es (frac{ad}{bc}).

Este método es útil porque no requiere cambiar los valores de las fracciones, lo que puede ser más intuitivo para algunas personas. Sin embargo, es importante recordar que este método solo se aplica cuando se divide una fracción por otra.

Te puede interesar: Descubre cómo Mauricio preparó una refrescante limonada en su mercado ecológico.

Aplicación práctica del método de multiplicar en cruz

Para aplicar este método en la vida cotidiana, consideremos un ejemplo práctico. Supongamos que tenemos dos fracciones: (frac{2}{3}) y (frac{4}{5}). Para dividir estas fracciones, multiplicamos el numerador de la primera fracción ((2)) por el denominador de la segunda fracción ((5)), obteniendo (10). Luego, multiplicamos el denominador de la primera fracción ((3)) por el numerador de la segunda fracción ((4)), obteniendo (12). El resultado final es (frac{10}{12}), que se puede simplificar a (frac{5}{6}).

Método 2: Invertir y multiplicar

El segundo método para dividir fracciones es conocido como "invertir y multiplicar". Este método implica invertir la segunda fracción, cambiando su numerador y denominador, y luego multiplicar las dos fracciones. Este método puede ser más intuitivo para algunas personas porque no requiere recordar reglas adicionales.

Para ilustrar este método, consideremos nuevamente las fracciones (frac{a}{b}) y (frac{c}{d}). Para dividir estas fracciones, primero invertimos la segunda fracción, obteniendo (frac{d}{c}). Luego, multiplicamos la primera fracción por la fracción invertida: (frac{a}{b} times frac{d}{c}). Esto resulta en (frac{ad}{bc}), que es el mismo resultado que obtuvimos con el método de multiplicar en cruz.

Aplicación práctica del método de invertir y multiplicar

Te puede interesar: Ángulos Obtusos: Todo lo que Necesitas Saber

Para aplicar este método en la vida cotidiana, consideremos el mismo ejemplo práctico anterior: (frac{2}{3}) y (frac{4}{5}). Primero, invertimos la segunda fracción, obteniendo (frac{5}{4}). Luego, multiplicamos la primera fracción por la fracción invertida: (frac{2}{3} times frac{5}{4}). Esto resulta en (frac{10}{12}), que se puede simplificar a (frac{5}{6}), el mismo resultado obtenido con el método de multiplicar en cruz.

Comparación de métodos

Ambos métodos, "multiplicar en cruz" y "invertir y multiplicar", son útiles y proporcionan resultados idénticos. Sin embargo, hay algunas diferencias clave entre ellos. El método de "multiplicar en cruz" es más directo y no requiere cambiar los valores de las fracciones, lo que puede ser más intuitivo para algunas personas. Por otro lado, el método de "invertir y multiplicar" puede ser más fácil de recordar porque no requiere reglas adicionales.

Ventajas y desventajas de cada método

El método de "multiplicar en cruz" tiene la ventaja de ser más directo y no requerir cambiar los valores de las fracciones. Sin embargo, puede ser menos intuitivo para algunas personas porque requiere recordar reglas adicionales. El método de "invertir y multiplicar" tiene la ventaja de ser más fácil de recordar y no requerir cambiar los valores de las fracciones. Sin embargo, puede ser menos intuitivo para algunas personas porque requiere invertir una fracción antes de multiplicarla.

Conclusión

Ambos métodos, "multiplicar en cruz" y "invertir y multiplicar", son útiles y proporcionan resultados idénticos. La elección del método depende de la preferencia personal y de la situación específica. Es importante recordar que estos métodos solo se aplican cuando se divide una fracción por otra.

Te puede interesar: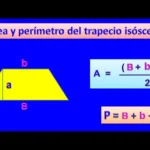 Cómo calcular el perímetro de un trapecio isósceles