Cómo resolver raíces cuadradas paso a paso

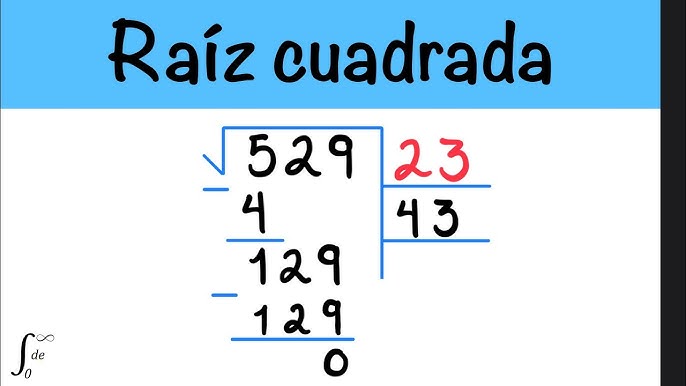
La metodología para resolver raíces cuadradas es una habilidad matemática fundamental que permite encontrar el valor de un número que, al ser multiplicado por sí mismo, da como resultado otro número. Este proceso puede parecer complejo al principio, pero con la práctica adecuada y una guía detallada, cualquiera puede dominarlo. En este artículo, exploraremos los pasos necesarios para resolver raíces cuadradas de manera efectiva y eficiente.

En primer lugar, es importante entender que la raíz cuadrada de un número es una operación inversa a la potencia cuadrada. Por ejemplo, si sabemos que ( 34 ) es el resultado de multiplicar dos números iguales, entonces la raíz cuadrada de ( 34 ) sería uno de esos números. Este concepto se aplica a cualquier número positivo y es crucial en diversas áreas de las matemáticas, desde la geometría hasta la estadística.

Método para resolver raíces cuadradas

Para resolver una raíz cuadrada, es necesario seguir un método sistemático que nos permita encontrar el valor correcto de manera precisa. Este método implica la realización de varios pasos secuenciales que nos llevan a descomponer el número original en partes más manejables.

Paso 1: Identificación del número

El primer paso es identificar el número cuya raíz cuadrada deseamos encontrar. Este número debe ser positivo, ya que las raíces cuadradas de números negativos no son reales. Por ejemplo, si queremos encontrar la raíz cuadrada de ( 34 ), comenzamos con este número.

Paso 2: Descomposición del número

El siguiente paso es descomponer el número en partes más manejables. Esto se hace dividiendo el número en dos partes, una que sea un múltiplo de ( 10 ) y otra que no lo sea. Por ejemplo, para ( 34 ), podemos separarlo en ( 30 ) (múltiplo de ( 10 )) y ( 4 ) (resto).

Te puede interesar: "Resuelve Ecuaciones: Guía Paso a Paso"

Paso 3: Encontrar la raíz cuadrada del múltiplo de 10

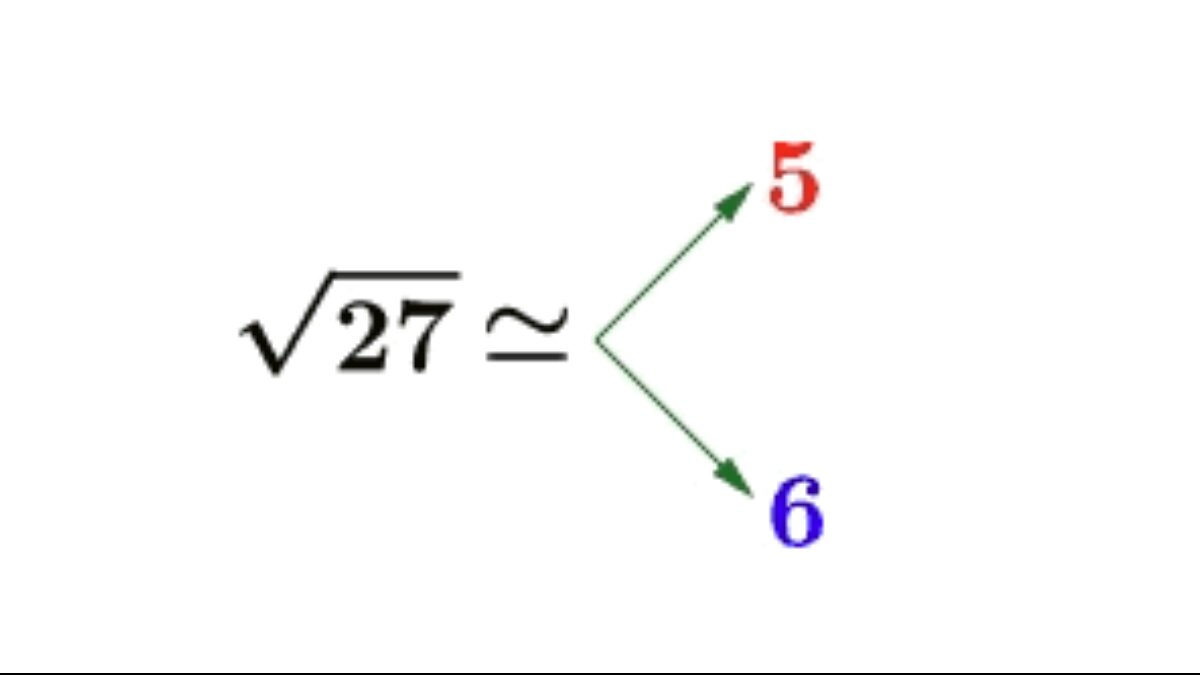
La raíz cuadrada de un múltiplo de ( 10 ) es fácil de encontrar porque se puede descomponer en un número que termina en ( 0 ) y otro que termina en ( 5 ). Por ejemplo, la raíz cuadrada de ( 30 ) es ( 5 ), ya que ( 5 times 5 = 25 ) y ( 6 times 6 = 36 ), por lo que la raíz cuadrada de ( 30 ) es aproximadamente ( 5.5 ).

Paso 4: Encontrar la raíz cuadrada del resto

Para encontrar la raíz cuadrada del resto, utilizamos un método de prueba y error. Probamos diferentes números hasta encontrar uno que, al ser multiplicado por sí mismo, se acerque al resto sin excederlo. Por ejemplo, para ( 4 ), probamos ( 2 ) porque ( 2 times 2 = 4 ).

Ejemplo paso a paso

Para ilustrar el método, consideremos el siguiente ejemplo:

Paso 1: Identificación del número

Supongamos que queremos encontrar la raíz cuadrada de ( 34 ).

Te puede interesar: Descubre los símbolos matemáticos: >, <, = y más

Paso 2: Descomposición del número

Separamos ( 34 ) en ( 30 ) (múltiplo de ( 10 )) y ( 4 ) (resto).

Paso 3: Encontrar la raíz cuadrada del múltiplo de 10

La raíz cuadrada de ( 30 ) es aproximadamente ( 5.5 ), ya que ( 5 times 5 = 25 ) y ( 6 times 6 = 36 ).

Paso 4: Encontrar la raíz cuadrada del resto

Para ( 4 ), probamos ( 2 ) porque ( 2 times 2 = 4 ).

Encontrar la raíz cuadrada de un número más grande

Para números más grandes, el proceso es similar pero con más pasos intermedios. Por ejemplo, para encontrar la raíz cuadrada de ( 100 ), descomponemos ( 100 ) en ( 100 ) (múltiplo de ( 10 )) y ( 0 ) (resto). La raíz cuadrada de ( 100 ) es ( 10 ), ya que ( 10 times 10 = 100 ).

Te puede interesar: Cómo sumar fracciones: guía para estudiantes de primaria

Conclusión

La resolución de una raíz cuadrada implica un proceso sistemático y secuencial que nos permite descomponer el número original en partes más manejables. Este método es aplicable a cualquier número positivo y es fundamental para entender las relaciones entre números y sus raíces cuadradas. Con práctica, cualquiera puede dominar este método y resolver raíces cuadradas de manera efectiva.