Descubre los Monomios: Componentes y Propiedades

En matemáticas, un monomio es una expresión algebraica que se compone de números y letras relacionados únicamente por multiplicaciones. Los monomios son fundamentales en el estudio del álgebra y tienen aplicaciones importantes en diversas ramas de las matemáticas, como la geometría y el análisis. En este artículo, exploraremos en detalle qué es un monomio, sus componentes y propiedades, así como cómo identificar y trabajar con ellos.

Un monomio se diferencia de otros tipos de expresiones algebraicas por su simplicidad y estructura. Por ejemplo, -5ax³ es un monomio, mientras que -2m5 + m3 no lo es debido a la presencia de sumas y restas. Este artículo tiene como objetivo proporcionar una comprensión profunda de los monomios, sus partes constituyentes y cómo se utilizan en el contexto matemático.

Definición de Monomio

Un monomio es una combinación de números y letras relacionados únicamente por multiplicaciones, con exponentes naturales. En otras palabras, un monomio es una expresión algebraica que no contiene ni sumas ni restas. Los monomios son los bloques básicos de las expresiones algebraicas más complejas, como los polinomios y los polinomios de varias variables.

Para entender mejor la definición de un monomio, consideremos algunos ejemplos. La expresión 4xy es un monomio porque se compone de los números 4 y las letras x e y, relacionados por multiplicación. Por otro lado, la expresión 3x + 2y no es un monomio porque contiene una suma. Es importante destacar que los monomios pueden tener coeficientes negativos, como en el caso de -5ax³, pero siempre deben estar relacionados únicamente por multiplicaciones.

Componentes del Monomio

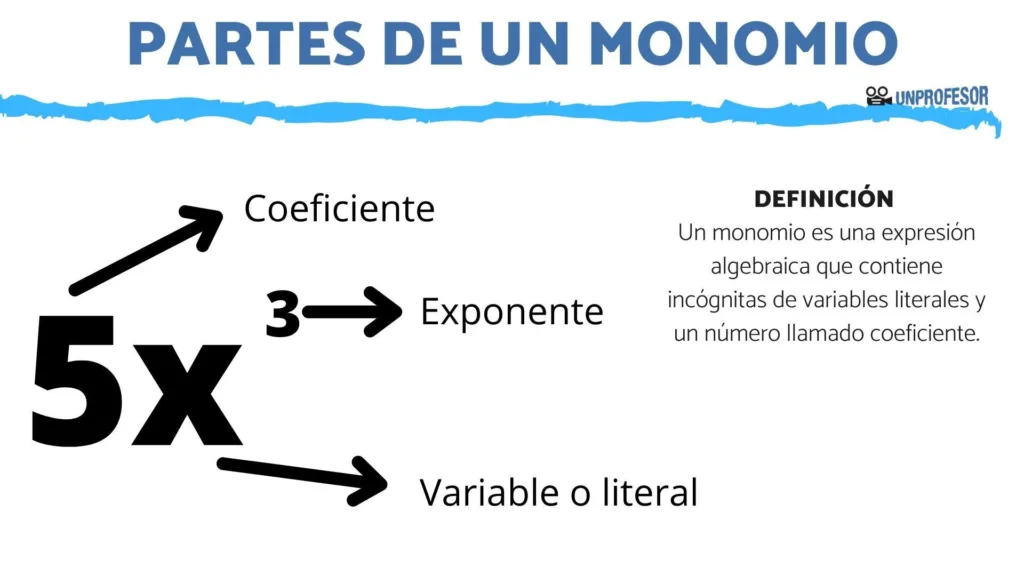
Un monomio está compuesto por varios componentes esenciales que trabajan juntos para formar una expresión algebraica simple y coherente. Estos componentes son el coeficiente, la parte literal y el grado. A continuación, se describirán cada uno de estos componentes en detalle.

Te puede interesar: "Descubre el poder de las potencias: resuelve problemas complejos de manera eficiente"

Coeficiente

El coeficiente es el número que multiplica las letras en un monomio. En la expresión 4xy, el coeficiente es 4 porque es el número que se multiplica con x e y. Los coeficientes pueden ser positivos o negativos, y también pueden ser fracciones o incluso números irracionales. Por ejemplo, en el monomio (frac{1}{2}xy), el coeficiente es (frac{1}{2}).

El coeficiente juega un papel crucial en la simplificación y manipulación de los monomios. Por ejemplo, al sumar o restar monomios, se deben considerar sus coeficientes para obtener el resultado correcto. El coeficiente es una parte fundamental del monomio que afecta su valor y su comportamiento en las operaciones algebraicas.

Parte Literal

La parte literal de un monomio es la combinación de letras y sus respectivos exponentes. En el monomio 4xy, la parte literal es xy porque son las letras que se multiplican por el coeficiente. Los exponentes indican cuántas veces se multiplica cada letra consigo misma. Por ejemplo, en el monomio (5x^2), la parte literal es (x^2) porque x se multiplica dos veces con sí mismo.

La parte literal puede contener una o más letras, y cada letra puede tener un exponente diferente. Por ejemplo, en el monomio (7m^3n^4), la parte literal es (m^3n^4) porque m se multiplica tres veces con sí mismo y n se multiplica cuatro veces con sí mismo. La parte literal es crucial para entender cómo se comportan los monomios en diferentes contextos matemáticos.

Grado

El grado de un monomio es la suma de los exponentes de las letras que aparecen en su parte literal. En el monomio (5x^2y), el grado es 2 + 1 = 3 porque se suman los exponentes de x y y. El grado indica el nivel o el orden del monomio en términos de sus letras y sus exponentes.

Te puede interesar: Propiedades asociativas en suma y multiplicación

El grado es una propiedad importante de los monomios porque determina su clasificación en polinomios y otras expresiones algebraicas. Por ejemplo, un polinomio de grado 2 se llama cuadrático, mientras que uno de grado 3 se llama cúbico. El grado también afecta cómo se comportan los monomios en operaciones como la suma y la resta.

Variable

En el contexto de los monomios, una variable es una letra que representa un número desconocido o variable. Las variables son fundamentales en los monomios porque permiten representar expresiones algebraicas generales que pueden aplicarse a diferentes valores. Por ejemplo, en el monomio (ax^2), la variable es a porque puede tomar diferentes valores dependiendo del contexto.

Las variables pueden ser de diferentes tipos, como las variables independientes y las variables dependientes. En los monomios, las variables son generalmente letras como x, y, z, etc., que representan números desconocidos en expresiones algebraicas. Las variables permiten que los monomios sean aplicables a una amplia gama de problemas matemáticos y científicos.

Grado

El grado de un monomio es la suma de los exponentes de las letras que aparecen en su parte literal. En el monomio (5x^2y), el grado es 2 + 1 = 3 porque se suman los exponentes de x y y. El grado indica el nivel o el orden del monomio en términos de sus letras y sus exponentes.

El grado es una propiedad importante de los monomios porque determina su clasificación en polinomios y otras expresiones algebraicas. Por ejemplo, un polinomio de grado 2 se llama cuadrático, mientras que uno de grado 3 se llama cúbico. El grado también afecta cómo se comportan los monomios en operaciones como la suma y la resta.

Te puede interesar: Cómo resolver raíces cuadradas paso a paso

Conclusión

Los monomios son expresiones algebraicas fundamentales que forman la base de muchas otras estructuras matemáticas. Comprender los componentes de un monomio, como el coeficiente, la parte literal y el grado, es crucial para manipular y resolver problemas algebraicos. Además, las variables y el grado juegan roles importantes en la clasificación y aplicación de los monomios en diversos contextos matemáticos. Los monomios son herramientas poderosas que permiten abordar una amplia gama de problemas en matemáticas y ciencias.