Descubre la regla secreta de las secuencias numéricas

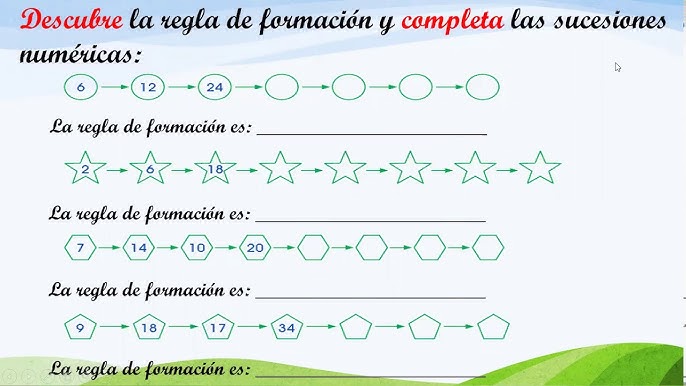
Las secuencias de números son una parte fundamental del estudio de las matemáticas y tienen aplicaciones en diversas áreas del conocimiento. Una secuencia numérica es un conjunto de números ordenados según una regla fija. Lo más difícil al trabajar con secuencias numéricas es encontrar la regla que las rige, ya que una vez hallada, solo se debe seguirla para encontrar los siguientes números de la secuencia. Para averiguar la regla, primero se debe determinar si la secuencia es ascendente, descendente o una combinación de ambas. Las secuencias ascendentes son donde cada número es mayor que el anterior y pueden ser de sumas (sumando 1), multiplicaciones (multiplicando por 2) o una combinación de ambas (alternando la suma de 4 con la multiplicación de 2). Las secuencias descendentes son donde cada número es menor que el anterior y pueden ser de restas (restando 3). El post incluye un ejercicio para encontrar la regla de una secuencia numérica, invitando a los lectores a compartir sus hallazgos. Además, se menciona el método para aprender más matemáticas de primaria.

¿Qué son las secuencias numéricas?

Las secuencias numéricas son conjuntos de números que siguen una regla específica. Estas secuencias pueden ser de cualquier longitud y pueden incluir tanto números positivos como negativos, así como números enteros o fracciones. Lo más importante al trabajar con secuencias numéricas es identificar la regla que las rige, ya que esta regla determina cómo se generan los siguientes números en la secuencia. Una vez que se ha encontrado la regla, se puede predecir el próximo número en la secuencia con bastante precisión.

Las secuencias numéricas tienen aplicaciones en diversas áreas del conocimiento, incluyendo la matemática recreativa, la teoría de números y la informática. En la matemática recreativa, las secuencias numéricas pueden ser utilizadas para resolver rompecabezas y acertijos. En la teoría de números, las secuencias numéricas pueden ser utilizadas para estudiar propiedades de los números, como su divisibilidad o su representación en diferentes bases numéricas. En la informática, las secuencias numéricas son fundamentales para el diseño de algoritmos y la programación.

Tipos de secuencias numéricas

Las secuencias numéricas pueden clasificarse en varios tipos según la regla que las rige. Los principales tipos de secuencias numéricas son:

Te puede interesar: "Descubre Unidades, Decenas y Centenas: Ejemplos y Valor Posicional"

Secuencias ascendentes

Las secuencias ascendentes son aquellas en las que cada número es mayor que el anterior. Estas secuencias pueden ser de sumas, multiplicaciones o una combinación de ambas. En las secuencias de suma, se añade un valor constante a cada número para obtener el siguiente. Por ejemplo, la secuencia 1, 2, 3, 4 es una secuencia de suma donde se añade 1 a cada número. En las secuencias de multiplicación, se multiplica un valor constante por cada número para obtener el siguiente. Por ejemplo, la secuencia 1, 2, 4, 8 es una secuencia de multiplicación donde se multiplica por 2 cada número. También es posible encontrar secuencias ascendentes que alternan entre sumas y multiplicaciones.

Secuencias descendentes

Las secuencias descendentes son aquellas en las que cada número es menor que el anterior. Estas secuencias suelen ser de restas, donde se resta un valor constante a cada número para obtener el siguiente. Por ejemplo, la secuencia 4, 3, 2, 1 es una secuencia de restas donde se resta 1 a cada número. Las secuencias descendentes pueden ser más complejas que las ascendentes, ya que requieren un análisis más detallado para determinar la regla que las rige.

Secuencias ascendentes

Las secuencias ascendentes son aquellas en las que cada número es mayor que el anterior. Estas secuencias pueden ser de sumas, multiplicaciones o una combinación de ambas. En las secuencias de suma, se añade un valor constante a cada número para obtener el siguiente. Por ejemplo, la secuencia 1, 2, 3, 4 es una secuencia de suma donde se añade 1 a cada número. En las secuencias de multiplicación, se multiplica un valor constante por cada número para obtener el siguiente. Por ejemplo, la secuencia 1, 2, 4, 8 es una secuencia de multiplicación donde se multiplica por 2 cada número. También es posible encontrar secuencias ascendentes que alternan entre sumas y multiplicaciones.

Ejemplo de secuencia ascendente

Te puede interesar: Aprende a calcular cuadrados mentalmente: trucos para números cerca de 50

Un ejemplo clásico de una secuencia ascendente es la secuencia de Fibonacci, donde cada número es la suma de los dos anteriores. La secuencia de Fibonacci comienza con 0 y 1, y cada número posterior es la suma de los dos anteriores. Por ejemplo, la secuencia de Fibonacci es 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, ... En esta secuencia, cada número es mayor que el anterior, y la regla que la rige es que cada número es la suma de los dos anteriores.

Secuencias descendentes

Las secuencias descendentes son aquellas en las que cada número es menor que el anterior. Estas secuencias suelen ser de restas, donde se resta un valor constante a cada número para obtener el siguiente. Por ejemplo, la secuencia 4, 3, 2, 1 es una secuencia de restas donde se resta 1 a cada número. Las secuencias descendentes pueden ser más complejas que las ascendentes, ya que requieren un análisis más detallado para determinar la regla que las rige.

Ejemplo de secuencia descendente

Un ejemplo clásico de una secuencia descendente es la secuencia de números naturales en orden inverso. Por ejemplo, la secuencia 5, 4, 3, 2, 1 es una secuencia descendente donde se resta 1 a cada número para obtener el siguiente. En esta secuencia, cada número es menor que el anterior, y la regla que la rige es que se resta 1 a cada número para obtener el siguiente.

Conclusión

Las secuencias numéricas son conjuntos de números que siguen una regla específica. Estas secuencias pueden ser ascendentes o descendentes, y la clave para trabajar con ellas es identificar la regla que las rige. Una vez que se ha encontrado la regla, se puede predecir el próximo número en la secuencia con bastante precisión. Las secuencias numéricas tienen aplicaciones en diversas áreas del conocimiento, incluyendo la matemática recreativa, la teoría de números y la informática.

Te puede interesar: El valor posicional: clave para entender operaciones matemáticas