Descubre la Simetría: Tipos y Aplicaciones
La simetría es un concepto fundamental en la geometría y las matemáticas que se refiere a la relación de igualdad entre dos o más figuras, objetos o entidades. Esta relación se establece cuando es posible transformar una figura en otra mediante movimientos como traslaciones, rotaciones o reflexiones. La simetría puede encontrarse en diferentes formas y contextos, tanto en la vida cotidiana como en el arte y la naturaleza.
La simetría no solo es un concepto matemático, sino que también tiene aplicaciones prácticas en diversas disciplinas. En este artículo, exploraremos los diferentes tipos de simetría y sus aplicaciones en la vida cotidiana, el arte y la naturaleza. Además, abordaremos algunos ejercicios relacionados con la simetría para ilustrar su importancia y utilidad.
Tipos de Simetría
Simetría Axial (o Refleja)
La simetría axial es uno de los tipos más comunes de simetría. Se produce con respecto a una línea recta llamada eje de simetría. Cuando una figura tiene un eje de simetría, puede ser dividida en dos partes iguales por este eje. Un ejemplo clásico de la simetría axial es un espejo, donde la imagen se refleja en el eje vertical. En la vida cotidiana, podemos encontrar esta simetría en objetos como puertas, ventanas y espejos.
Simetría Rotacional (o Giratoria)
La simetría rotacional se produce cuando una figura no cambia al girarla un ángulo determinado. Este tipo de simetría es común en figuras geométricas como estrellas y círculos. Por ejemplo, una estrella de cuatro puntas no cambia su apariencia si se gira 90 grados (u cualquier múltiplo de 90 grados). En la naturaleza, muchos animales y plantas exhiben simetría rotacional en sus cuerpos.
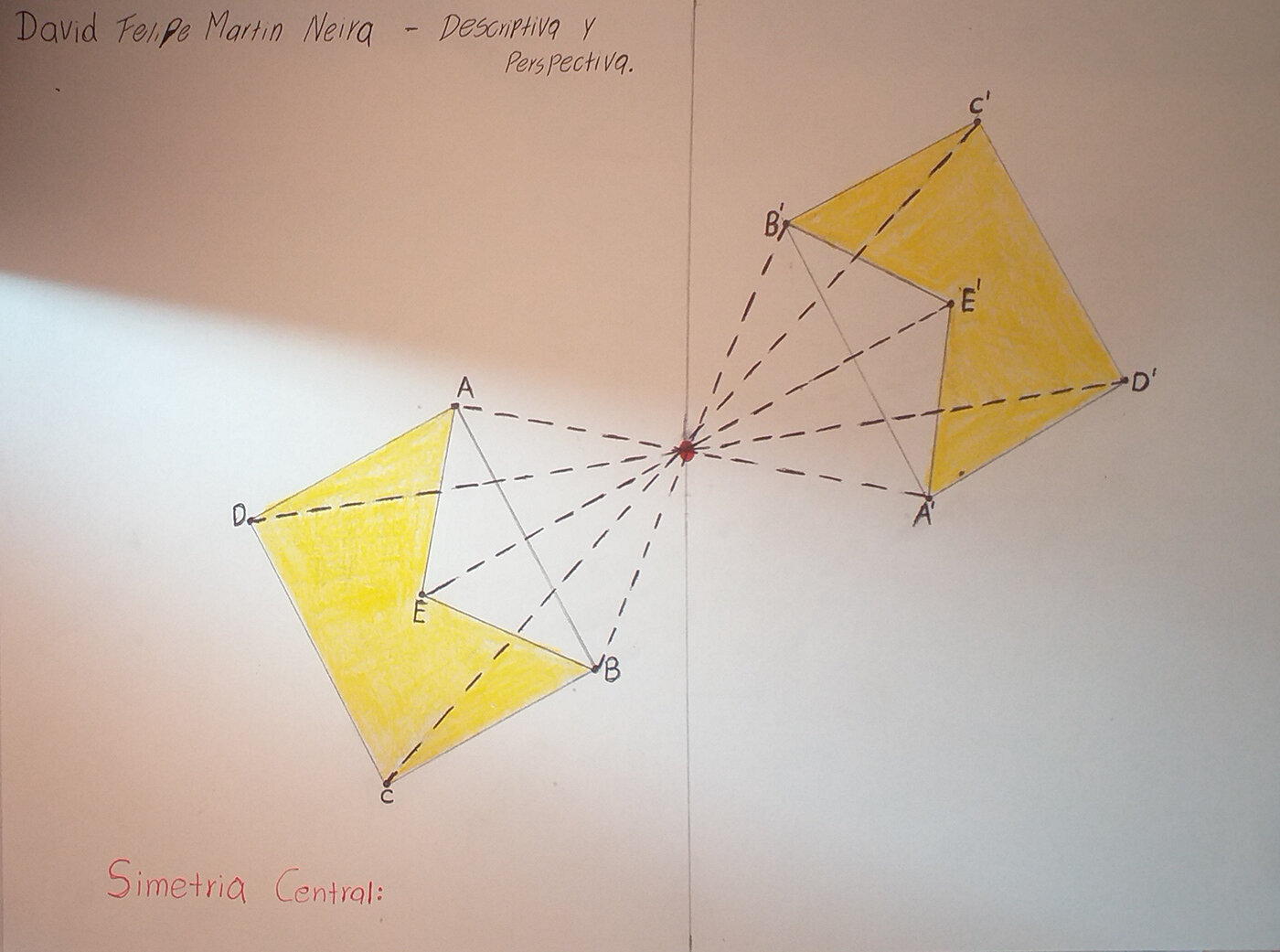
Simetría Central
Descubre los secretos de los prismas: bases, caras laterales y volumenLa simetría central es menos común que los otros tipos. Dos puntos son simétricos respecto un punto llamado centro de simetría. Este tipo de simetría se encuentra en figuras como una flor de cuatro punta, que puede ser girada 180 grados y seguir siendo la misma figura. En el arte, las esculturas a menudo utilizan la simetría central para crear figuras equilibradas y estéticamente agradables.
Aplicaciones de la Simetría
En la Vida Cotidiana
La simetría es omnipresente en nuestra vida diaria. Nuestro cuerpo, por ejemplo, está dividido en dos partes simétricas: izquierda y derecha. Además, muchos objetos de uso cotidiano como sillas, mesas y ventanas también exhiben simetría. La simetría no solo es estética, sino que también tiene funciones prácticas. Por ejemplo, las puertas y ventanas son más fáciles de abrir y cerrar gracias a su diseño simétrico.
En el Arte
El arte es otra área donde la simetría juega un papel crucial. Desde la antigüedad, los artistas han utilizado la simetría para crear obras equilibradas y armoniosas. Las pinturas, esculturas y música a menudo se basan en principios de simetría para lograr un efecto estético. En la música, por ejemplo, las canciones a menudo tienen una estructura simétrica con versos y coros que se repiten de manera equilibrada.
En la Naturaleza
La naturaleza también ofrece numerosos ejemplos de simetría. Desde los pétalos de una flor hasta las alas de un insecto, muchas estructuras naturales exhiben simetría axial o rotacional. La simetría en la naturaleza no solo es estética, sino que también tiene funciones prácticas. Por ejemplo, las alas de un ave son simétricas para facilitar el vuelo y la navegación.
Te puede interesar:
Teorema de Pitágoras: Demostración y AplicacionesEjercicios de Simetría en Matématica App
En la Vida Cotidiana
Para ilustrar la importancia de la simetría, podemos realizar ejercicios prácticos en la vida cotidiana. Por ejemplo, podemos dibujar una puerta y luego dividirla en dos partes iguales con un eje de simetría. Este tipo de actividad ayuda a comprender cómo funciona la simetría axial.
En el Arte
En el ámbito del arte, podemos realizar ejercicios de dibujo y pintura utilizando principios de simetría. Por ejemplo, podemos crear un mandala con simetría rotacional o una composición equilibrada con simetría central. Estos ejercicios no solo son divertidos, sino que también enseñan a apreciar la belleza y el orden que la simetría aporta al mundo.
En la Naturaleza
En la naturaleza, podemos observar y dibujar estructuras naturales como hojas, flores y animales para identificar sus ejes de simetría. Este tipo de actividad no solo es educativa, sino que también fomenta el interés por la ciencia y la naturaleza.
Conclusión
La simetría es un concepto fundamental en las matemáticas y la geometría. Se puede aplicar en muchas áreas de la vida cotidiana, el arte y la naturaleza. Es importante comprender los diferentes tipos de simetría y cómo se aplican en diversos contextos para poder resolver problemas y apreciar la belleza y orden que la simetría aporta al mundo.
Te puede interesar:
Descubriendo el Trapezoide: Un Cuadrilátero Menos ConocidoSi quieres seguir aprendiendo geometría y matemáticas de primaria, adaptadas a tu nivel, entra en Matématica App, regístrate y prueba gratis.
Deja un comentario
Posts Interesantes