Explorando Problemas de Operaciones Combinadas: Aditivas, Multiplicativas y Mixtas

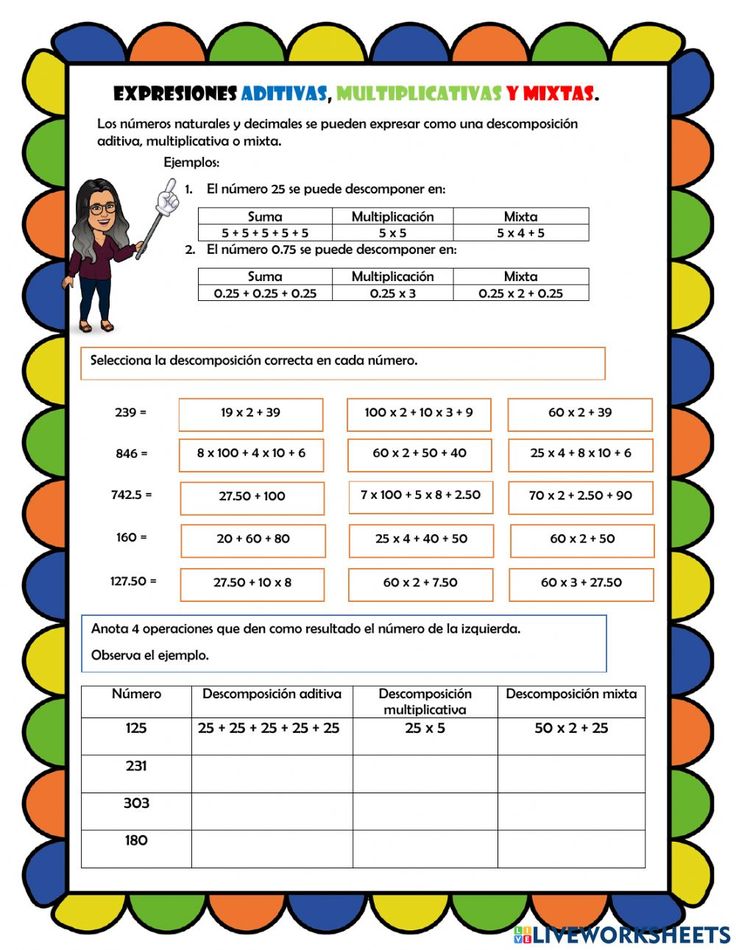
En el ámbito de la resolución de problemas matemáticos, es fundamental comprender las diferentes estructuras que pueden presentarse. Hoy hemos explorado diferentes tipos de problemas de operaciones combinadas, que se dividen según las operaciones necesarias para resolverlos. Los problemas de estructura aditiva pura implican sumas y restas, mientras que los de estructura multiplicativa pura involucran multiplicaciones y divisiones. Por último, los problemas de estructura mixta combinan ambas operaciones. Para resolver estos problemas, a veces es útil formular preguntas intermedias que faciliten el proceso.

En esta exploración, hemos visto cómo las preguntas intermedias pueden ser cruciales para descomponer un problema complejo en partes más manejables. Por ejemplo, en un problema aditivo puro, podemos preguntarnos cuánto habría pagado Tomás sin descuento, y en uno multiplicativo puro, cuántos niños han montado en "La rueda loca". En los problemas mixtos, como el del pirata Barba Plata, es necesario descomponer el problema en varias preguntas intermedias para llegar a la solución final.

Problemas de Estructura Aditiva Pura

Los problemas de estructura aditiva pura se caracterizan por involucrar únicamente operaciones de suma y resta. Estos problemas son relativamente simples en comparación con los otros tipos, pero aún así pueden presentar desafíos interesantes. Un ejemplo clásico es el problema de determinar cuánto dinero se recaudó en una venta después de aplicar un descuento.

Formulación de Preguntas Intermedias

Para resolver problemas aditivos puros, es útil formular preguntas intermedias que faciliten el proceso. Por ejemplo, si se sabe que Tomás pagó $100 por un artículo con un 20% de descuento, podemos preguntarnos cuánto habría pagado sin el descuento. Esto nos lleva a la pregunta intermedia: ¿Cuál es el precio original del artículo?

Ejemplos de Problemas Aditivos Puros

Un ejemplo típico de un problema aditivo puro es el siguiente: "Si Tomás pagó $100 por un artículo con un 20% de descuento, ¿cuál es el precio original del artículo?". Para resolver este problema, primero debemos determinar cuánto habría costado el artículo sin el descuento. Esto implica encontrar el valor original antes de aplicar la reducción del 20%.

Problemas de Estructura Multiplicativa Pura

Los problemas de estructura multiplicativa pura se centran en operaciones de multiplicación y división. Estos problemas pueden ser más complejos debido a la naturaleza de las operaciones involucradas. Un ejemplo común es determinar cuántos niños han montado en una atracción llamada "La rueda loca" durante un día específico.

Formulación de Preguntas Intermedias

Para resolver problemas multiplicativos puros, también es útil formular preguntas intermedias. Por ejemplo, si se sabe que cada niño monta en "La rueda loca" dos veces por hora y que la atracción funciona durante ocho horas, podemos preguntarnos cuántos niños han montado en total. Esto nos lleva a la pregunta intermedia: ¿Cuántos niños montan en una hora?

Ejemplos de Problemas Multiplicativos Puros

Un ejemplo típico de un problema multiplicativo puro es el siguiente: "Si cada niño monta en 'La rueda loca' dos veces por hora y la atracción funciona durante ocho horas, ¿cuántos niños han montado en total?". Para resolver este problema, primero debemos determinar cuántos niños montan en una hora. Luego, multiplicamos este número por el número de horas que la atracción funciona.

Problemas de Estructura Mixta

Los problemas de estructura mixta combinan operaciones aditivas y multiplicativas. Estos problemas pueden ser los más complejos debido a la necesidad de manejar múltiples tipos de operaciones. Un ejemplo clásico es el problema del pirata Barba Plata, que involucra tanto sumas como divisiones para determinar cuánto oro le corresponde a cada pirata.

Formulación de Preguntas Intermedias

Para resolver problemas mixtos, es crucial descomponer el problema en varias preguntas intermedias. Por ejemplo, si se sabe que Barba Plata tiene 100 monedas de oro y que hay cinco piratas, podemos preguntarnos cuánto oro le corresponde a cada pirata. Esto nos lleva a la pregunta intermedia: ¿Cuánto oro le corresponde a cada pirata?

Ejemplos de Problemas Mixtos

Un ejemplo típico de un problema mixto es el siguiente: "Si Barba Plata tiene 100 monedas de oro y hay cinco piratas, ¿cuánto oro le corresponde a cada pirata?". Para resolver este problema, primero debemos determinar cuánto oro le corresponde a cada pirata. Luego, dividimos el total de monedas de oro entre el número de piratas para encontrar la cantidad de oro por pirata.

Conclusión

Los problemas aditivos puros, multiplicativos puros y mixtos presentan desafíos únicos que requieren diferentes enfoques para resolver. La clave para abordar estos problemas es formular preguntas intermedias que descomponen el problema en partes más manejables. Esto no solo facilita la resolución del problema, sino que también proporciona una mejor comprensión de los conceptos subyacentes.