Convertir 2/4 a Decimal: Resultado y Ejemplos Prácticos
La conversión de fracciones a números decimales es una habilidad matemática fundamental que se utiliza en diversas áreas, como la física, la ingeniería y las matemáticas financieras. En este artículo, nos enfocaremos en una de las conversiones más comunes: convertir 2/4 a decimal. Aunque parece una tarea sencilla, muchos estudiantes y profesionales pueden encontrar dificultades al realizar esta conversión. Aquí, exploraremos el resultado de convertir 2/4 a decimal, junto con ejemplos prácticos que ilustran el proceso con claridad.
El sistema numérico binario y el número 10
El sistema numérico binario es un sistema de numeración que utiliza solo dos dígitos: 0 y 1. Este sistema es fundamental en la informática y la electrónica digital, ya que los computadores y dispositivos electrónicos utilizan los dígitos binarios para procesar y almacenar información.
En el sistema decimal, que es el sistema numérico que utilizamos comúnmente, el número 10 se escribe como 10. Sin embargo, en el sistema binario, el número 10 se escribe como 2^3 + 2^1, que es igual a 8 + 2, que a su vez es igual a 10.
La representación binaria del número 10
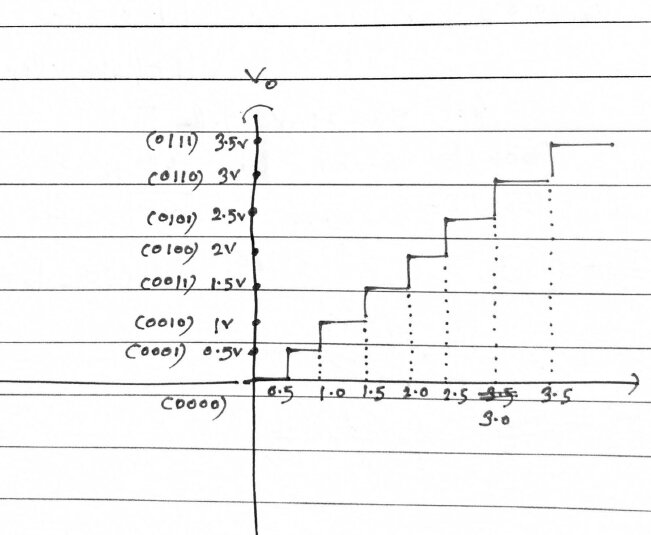
La representación binaria del número 10 es 1010. Esta representación se obtiene mediante la conversión del número decimal 10 a binario utilizando la fórmula mencionada anteriormente.
| Decimal | Binario |
|---|---|
| 10 | 1010 |
La importancia del número 10 en la informática
El número 10 es un número fundamental en la informática, ya que es la base del sistema decimal que se utiliza comúnmente en la programación y el procesamiento de datos. Además, el número 10 es también importante en el sistema binario, ya que es el resultado de la suma de los dígitos binarios 1010.
Te puede interesar:
Números Romanos del 1 al 200: Guía Práctica y Conversión FácilLa relación entre el sistema binario y el sistema decimal
El sistema binario y el sistema decimal están estrechamente relacionados, ya que el sistema binario es una representación en base 2 del sistema decimal. Cada dígito binario puede ser convertido a su equivalente decimal y viceversa.
La aplicación del número 10 en la vida real
El número 10 tiene una gran cantidad de aplicaciones en la vida real, desde la programación y el desarrollo de software hasta la electrónica y la ingeniería. Por ejemplo, en la programación, el número 10 se utiliza comúnmente como un valor predeterminado para variables y como un umbral para tomar decisiones.
La representación del número 10 en otros sistemas numéricos
El número 10 también puede ser representado en otros sistemas numéricos, como el sistema octal y el sistema hexadecimal. En el sistema octal, el número 10 se escribe como 12, mientras que en el sistema hexadecimal, se escribe como A.
¿Cuál es el proceso para convertir una fracción a un número decimal?
El proceso para convertir una fracción a un número decimal es relativamente sencillo. Lo primero que debemos hacer es dividir el numerador (el número que está encima de la línea de la fracción) entre el denominador (el número que está debajo de la línea de la fracción). En el caso de la fracción 2/4, debemos dividir 2 entre 4. La respuesta a esta división es el número decimal que estamos buscando.
¿Por qué es importante convertir fracciones a números decimales?
Convertir fracciones a números decimales es importante porque los números decimales son más fáciles de manejar y entender en la vida cotidiana. Los números decimales se utilizan en una amplia variedad de contextos, como en la cocina, en la construcción, en la ciencia y en la economía. Además, los números decimales son más precisos que las fracciones, lo que significa que pueden expresar cantidades más pequeñas y más exactas. Por ejemplo, si estamos haciendo una receta y necesitamos 1/4 de taza de harina, es más fácil medir 0,25 tazas que tratar de medir una fracción de taza.
Te puede interesar:
Figuras Geométricas para Niños: Imprimir y Recortar Gratis¿Cuál es la relación entre las fracciones y los números decimales?
Las fracciones y los números decimales están estrechamente relacionados. De hecho, los números decimales son simplemente una forma diferente de expresar una fracción. Por ejemplo, la fracción 1/2 es igual al número decimal 0,5. La fracción 3/4 es igual al número decimal 0,75. En general, una fracción se puede convertir a un número decimal dividiendo el numerador entre el denominador.
¿Cómo se puede convertir una fracción mixta a un número decimal?
Una fracción mixta es una fracción que tiene un numerador mayor que el denominador. Por ejemplo, la fracción mixta 2 3/4 es igual a 2 + 3/4. Para convertir una fracción mixta a un número decimal, debemos primero convertir la parte fraccionaria (3/4) a un número decimal y luego sumarla a la parte entera (2). En este caso, 3/4 es igual a 0,75, por lo que la fracción mixta 2 3/4 es igual a 2 + 0,75 = 2,75.
¿Cuáles son algunos ejemplos prácticos de convertir fracciones a números decimales?
Hay muchos ejemplos prácticos de convertir fracciones a números decimales. Uno de los ejemplos más comunes es en la cocina. Por ejemplo, si una receta requiere 1/4 de taza de azúcar, podemos convertir esta fracción a un número decimal dividiendo 1 entre 4, lo que nos da 0,25 tazas. Otro ejemplo es en la construcción, donde podemos necesitar convertir fracciones de metros a números decimales para calcular la longitud de una habitación o el área de un patio. En la economía, también podemos necesitar convertir fracciones de monedas a números decimales para calcular el cambio o el interés.
Curiosidades
¿Cuál es el valor decimal de 24 en base hexadecimal?
El valor hexadecimal 24 en decimal es 36. Para convertir un número hexadecimal a decimal, debemos considerar que cada dígito hexadecimal representa una potencia de 16. En este caso, el 2 representa 2 × 16^1 = 32 y el 4 representa 4 × 16^0 = 4. Sumando ambos valores, obtenemos 36. Es importante recordar que la notación hexadecimal se utiliza comúnmente en programación y sistemas informáticos.
¿Cómo se puede convertir 24 en hexadecimal a binario?
Para convertir el valor hexadecimal 24 a binario, debemos convertir cada dígito hexadecimal a su equivalente binario. El 2 en hexadecimal es 10 en binario y el 4 en hexadecimal es 100 en binario. Por lo tanto, el valor hexadecimal 24 se convierte en 10100 en binario. Es importante destacar que la notación binaria es la base 2 y se utiliza comúnmente en sistemas informáticos y electrónica.
Te puede interesar:
El Teorema de Tales: Solucionando Problemas de Geometría con Éxito¿Cuál es el uso más común del valor hexadecimal 24?
El valor hexadecimal 24 se utiliza comúnmente en programación y desarrollo web para representar colores. En el sistema de color hexadecimal, cada par de dígitos representa la intensidad de los colores rojo, verde y azul. En este caso, el valor hexadecimal 24 se puede utilizar para representar un tono de gris. Los valores hexadecimales se utilizan para definir colores en estilos CSS y otros lenguajes de programación.
¿Cuál es la relación entre el valor hexadecimal 24 y el sistema numérico decimal?
El valor hexadecimal 24 está relacionado con el sistema numérico decimal porque ambos sistemas utilizan diferentes bases para representar números. El sistema decimal utiliza una base 10, mientras que el sistema hexadecimal utiliza una base 16. La relación entre ambos sistemas se establece a través de la conversión de números entre una base y otra. En este caso, el valor hexadecimal 24 se puede convertir al valor decimal 36, lo que permite una comunicación efectiva entre sistemas que utilizan diferentes bases numéricas.
Posts Interesantes